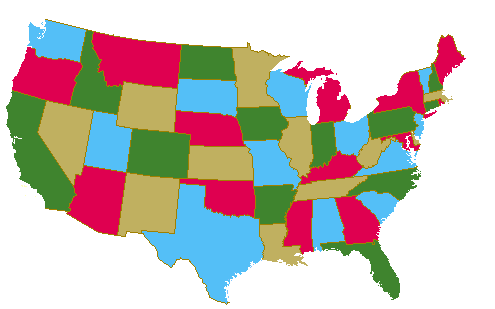
Map Wars - Can you color in the entire map?
Players: 2-4
Ages: 5 and up
Cost: Free!
Math Ideas: Spatial reasoning, graph theory
Questions to Ask:
Which states can you no longer color in?
If we work together, could we color in the whole map?
Could you create your own map?
I love a game where a child's intuition can lead them down a path toward a mathematical discovery. The easier the on-ramp into a mathematical game, the likelier a child is to find their own patterns and make their own discoveries.
Last week, I shared a puzzle game called Don't Connect the Dots! that provided a kid-friendly introduction to the rich mathematical world of graph theory. This week I'll be sharing another game, Map Wars, that is more deeply related to Don't Connect the Dots! than you might expect at first.
How to Play
The strategy of Map Wars changes significantly based on the number of players (2, 3, or 4), but each variation has its own fun and challenges.
Let's say you're playing with two players. Each person gets a marker or colored pencil. Print out a blank map of the US or any other complex map.
The two players take turns coloring in states with their markers. The only catch is, you cannot color two adjacent states with the same color.
Eventually, a player will run out of available states to color in, at which point they retire. When both players run out of states, the game is over. Add up your states to see who the winner is.
Once you've played the game competitively, it's fun to play a version cooperatively. Can two people, working together, color in the whole map using the guidelines of the game? Can three? Four?
Where's the Math?
Believe it or not, the questions above have been explored deeply by mathematicians for over a century.
In math, sometimes viewing the same problem from a different perspective can lead to new insights. So let's try to simplify the game.
We could color in each state fully, but that's not really necessary. So instead, let's just make a little circle at the center of each state that we will fill in with the appropriate color.
But how should we designate the adjacent states? We simply connect those dots with lines to show that, for example, Alabama is connected to Florida, Mississippi, Tennessee, and Georgia.
Step back from your completed map and what do you have? A giant puzzle just like the ones you solved in Don't Connect the Dots! Now you have a puzzle with 50 dots and a whole bunch of lines connecting them. So what is the chromatic number of the United States?
You may have noticed that none of the lines cross each other - this is a feature of all maps. If you try to imagine a counterexample, you'll realize that it is a geographic impossibility. The closest spot is the famous Four Corners in the western United States, but the states that are diagonal don't actually share a border. Colorado and Arizona are across a vertex from each other, but they don't count as adjacent states.
As it turns out, as long as none of the lines in a graph puzzle cross each other, the puzzles have a chromatic number of four or less. This means that all maps, no matter how complex, can be colored using only four colors.
This is known, fittingly, as the Four Color Theorem, and it is explained in further detail in this great Numberphile video.
Once you and your child know this theorem, you can test it out on all sorts of maps. The map of all the counties of England is a great challenge, and it's actually the map that inspired this math exploration in the first place!
Most interestingly to me, Map Wars and Don't Connect the Dots! seem different at first, but their underlying structure is exactly the same. Math is a wonderful tool for discovering the connections that bind together seemingly separate ideas. I love when that happens.
Questions to Ask
If you are playing competitively with your kids, you can spice up the game by asking them to think ahead to their next moves. "Now that you've colored in this state, what states can you no longer color in?" This will get your kids into a more strategic mindset, as they realize that each move they make constrains their further options.
If you are playing cooperatively, you should frame the task with the question "If we work together, could we color in the whole map?" Then you can test your mettle with two colors, then three, then four. It would be fun to see if you can identify the most US states that can be colored with two colors. I got 29 when I quickly played the game myself; can you beat me? Send me a picture if you do!
Once you've played on the US map a few times, you can always get out new maps and see whether they can all be colored in with four colors. Or, even better, ask your kids "Can we make our own maps?"
Then you can construct, copy, and trade maps with each other. Try to give your kids a challenging map, and remember: no matter how complex, every map can be colored in using only four colors.
This is the sort of game you might play with your kids one afternoon and then forget entirely, only to see them two months later, coloring in a map of their own design. Those are the moments that I dream of, the moments that inspire me to write this newsletter each week.