Don't Connect the Dots! — Games for Young Minds

Players: 1 or more
Ages: 5 and up
Cost: Free!
Math Ideas: Spatial reasoning, classification
Questions to Ask:
What is the fewest number of colors you need to fill in this puzzle?
Can you make a puzzle that requires 4 colors? What about 5? 6

In the past I've mentioned that I am teaching an elective at my middle school that is all about math games and mathematical artwork. My students have gotten to make origami, fractals like the Sierpinski Triangle and the Koch Snowflake (pictured), and stellated icosahedrons.

Since I have 29 kids in my room, I am always looking for cost-effective games that contain math ideas. So I was elated to come upon this wonderful post by Joel David Hamkins about teaching graph theory to seven-year-olds. I adapted some of his materials and turned them into a game I call Don't Connect the Dots!

How to Play

To start, you just need a pencil and a sheet of paper. On the paper, draw several small circles. Then, connect those circles to each other. There is no set rules - lines can cross, circles can connect to as many or as few other circles as you want (although the game is more fun and challenging if the circles are more interconnected).

Then, you get out some markers or colored pencils. Your goal is to fill in each circle with a color. The only restriction is, no circles that are connected by a line can contain the same color.

Now, the easiest way to "win" is to use a different color for each circle. Six circles, six colors. Simple! But the real challenge is to use as few colors as possible to complete your design.

Joel David Hamkins shared some great starting puzzles on his blog, but the real fun comes from creating and exploring your own puzzles with your kids.

Where's the Math?

Don't Connect the Dots, which is accessible enough for any elementary-age student to play, is in fact an introduction to graph theory, a university-level math course.

Graph theory is the sort of topic that terrified me when I was an undergrad. It seemed so esoteric and strange, sort of like that weird math problem that Matt Damon solves in Good Will Hunting.

But strip away the mathematical terminology, and you just have a bunch of dots connected by lines. The goal is to find the minimum number of colors that you can use to color in the dots, while making sure that none of the connected dots have the same color.

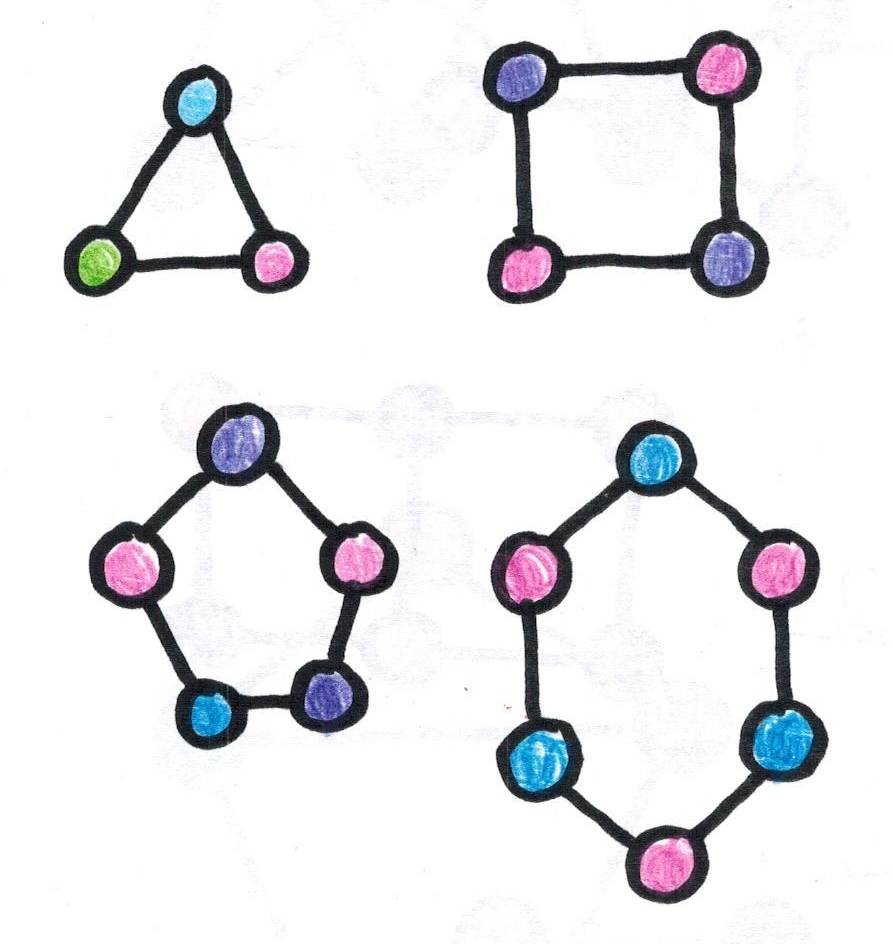
This is known as the chromatic number of a graph, and it's often smaller than you'd expect! For example, this image has five dots, but it only needs two colors.

I've had a lot of fun trying to figure out the chromatic number of a bunch of simple graph puzzles. For example, the most basic graph, which is two dots connected by a line, has a chromatic number of two. Add a third dot, and that triangle requires three colors. Add a fourth point to make a square and, surprisingly, the chromatic number goes back to two!

This pattern continues when you add five dots, six dots, and so on. Any loop of even dots has a chromatic number of two, and a loop of odd dots has a chromatic number of three.

If your child begins to explore these patterns and draw conclusions about types of graphs, they will be working on the heart of mathematics: creating hypotheses to explain patterns, and then trying to find a reason why these hypotheses are true.

So why do all the even loops have a chromatic number of two? That's a great question to ask your kid! Here are some more...

Questions to Ask

Kids tend to overestimate the number of colors that they'll need, so often they complete a graph with five colors when they could use four or three. In those situations, say "You solved this graph! Can you solve it again using fewer colors?"

By the way, it's important to ask that question even when they have solved the problem totally correctly! I know that seems weird, but there's a great reason for asking the same question regardless of your child's answer.

Let's say you ask your child what 4*5 is and they say 20! You might respond "Great!" But let's say instead they answer "25!" You respond: "Are you sure? Keep thinking"

In both cases, your child knows whether they got the answer right, but they haven't gotten a chance to explain their thought process, which is the most important part of mathematical thinking. Maybe they totally guessed when they answered 20, or maybe they misheard you when they answered 25.

So how do you unearth that information from your kids? You smile at their answers, right and wrong, and simply ask "How do you know?"

Now they can't glean from your question whether they are correct. They just have to explain their thought process. Once they do so, you are more than welcome to explain the correct answer. But more often than not, you'll learn much more about the thoughts that go into your kid's answers.

So in Don't Connect the Dots, ask your child "Can you solve it with fewer colors?" even if they can't, and wait for them to explain why they need three colors. Then tussle their hair and encourage them to solve the next one. Easy breezy.

Aside from that, the best and most creative question to ask your child is "Can you make a puzzle for me to solve?"

I did this with my students and my own kids, and I got such wonderful and varied problems! I love these problems so much that I made a worksheet with a bunch of student creations. There are problems with chromatic numbers of 2, 3, and 4, so they provide a nice challenge for your kids once they've solved their own. You can find a copy of this worksheet at this link.

I have a ton of extensions on this activity. In fact, I have so many that I'll be sharing a whole newsletter full of them next week! But in the mean time, I'll whet your appetite with the following questions for your kids:

Can you make a puzzle with a chromatic number of 4? 5? 7?
Can you draw a puzzle where every dot has three lines that connect to it? Can you draw a puzzle that meets that condition, but none of the lines can cross?