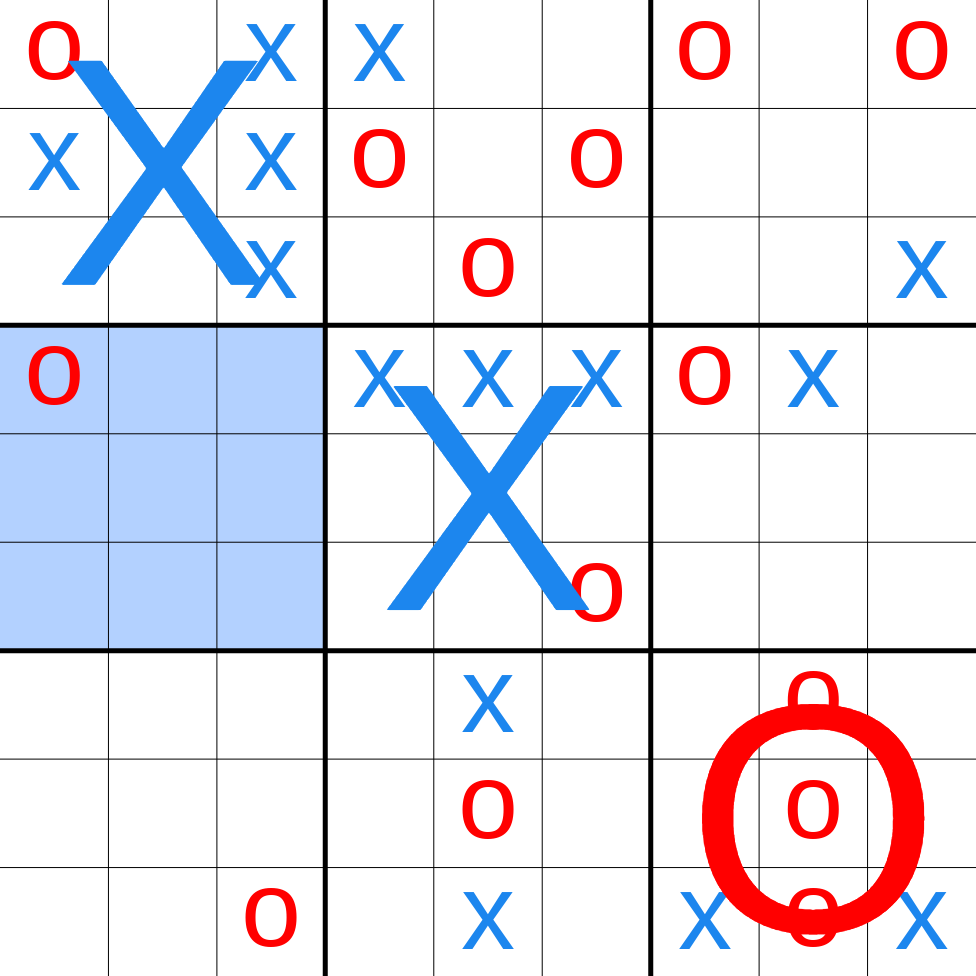
Ultimate Tic Tac Toe

Players: 2
Ages: 7 and up
Cost: Free! Just get a pencil and paper
Math Ideas: Deductive reasoning, proof
Questions to Ask: 
    If I play in this square, what game am I sending you to?

Periodically I pull out a math game in my 8th grade classes, usually when I have 20 minutes or so to kill after a field trip or standardized test.

In the past I've shared Magic Squares and The 100 Game, both of which I really enjoy introducing to my students. But I know how to beat both of those games, so I don't enjoy them as a participant in the same way that I enjoy games like chess or Blokus.

But there is one game I use with my students that captures my full attention: tic tac toe. But not the boring, solved version that you learned to beat when you were 6. I'm talking about Ultimate Tic Tac Toe.

How to Play

I discovered Ultimate Tic Tac Toe from Ben Orlin over at the wonderful website Math with Bad Drawings. I think Ben does some of the most interesting and entertaining art about math on the Internet, and his explanation of Ultimate Tic Tac Toe is characteristically clear and enjoyable. But I'll do my best to summarize here.

On a full piece of paper, draw a giant tic tac toe board that takes up the entire page. Then, in each of the nine squares of the big board, draw a smaller tic tac toe board. 

Players take turns marking squares with either an X or an O, just as in the normal game. If you win one of these smaller game, you capture that square in the larger board. Win three small games in a row, and you've won the game!

The real joy of the game, though, comes in this one extra rule: The square you choose to capture dictates where your opponent can play their next move.

Let's say you choose to play in the center game and mark an X in the upper lefthand corner of that game. Now your opponent must play in the upper lefthand game. If they play in the bottom righthand square, you must play in the bottom righthand game, and so on.

This might sound confusing, but it's really easy to follow once you've seen the game in action. I highly recommend the video below.
 

A couple of final rules are important: If you send your opponent to a game that has already been won, they are allowed to play anywhere on the board. And if one of the small games ends in a tie, it's not available to be captured for the overall game

Where's the Math?

In order to truly appreciate the math of this game, I'd ask that you play a round first. You can go ahead and teach it to your kid, or you can invite a friend to play on this free online version of the game.

If you play like most people, you'll probably start out by placing a bunch of Xs or Os around the board, more or less randomly. But as you get into later rounds, you'll realize that your moves are becoming constrained. You really want to play in a certain square, but if you do, you're sending your opponent to a game which she'll be able to win! 

But in order for her to win that game, she has to play in the center square, which will send you to the center game, which allows you to win that game! But then she'll be able to play down in that game, and so on. 

Your mind hops around the board from game to game, trying to anticipate several moves ahead. This sort of thinking sounds very familiar to a chess player. It's essentially logical deduction in game form.

Logical deduction is the process of using if-then reasoning to come to conclusions about a scenario. When your child looks at a geometry problem and thinks "This shape is a rectangle, and the top side is 12cm long, so the bottom side must also be 12cm long," they are using logical deduction. You start from a premise or two and then follow the thread of logic wherever it leads.

By giving your kids a fun, non-academic introduction to this habit of mind, you are helping them prepare for problem-solving both inside and outside of school. 

If you're lucky, your child will come to enjoy the process of logical deduction itself and begin to see these problems as a sort of game in and of itself. I certainly occupied my mind in math class by looking at the information I had and wondering "If this is true, what else can I prove?"

I'm not promising that your child will turn out to be as nerdy as I am. Honestly, let's hope they don't. But they might become a little more confident and comfortable with their skills of logical deduction.

Questions to Ask

The hardest element of Ultimate Tic Tac Toe is the fact that your moves dictate where your opponent can play. When you introduce the game to your child, I'd suggest repeatedly asking "If I play here, which board do you have to play on?"

Once your child is familiar with the basic mechanics of the game, you can start talking to them about the implications on gameplay. My favorite question to ask is "If you send me to this game, which square will I want to play in?" Lots of kids start playing a game focused only on their moves and their winning strategy. I like to push my students to alternately think about the game from their perspective and my own. Shifting back and forth between perspectives can often help kids gain new insights into a problem, and Ultimate Tic Tac Toe is no exception.

If your child gets really into the game, you can start expanding the scope of your questioning, using some of Ben Orlin's tic tac toe puzzles. In this post, Ben outlines some variations on tic tac toe that are fun to puzzle over, as well as his interpretation of the difference between a puzzle and a game. Like I said, I love this guy's writing, and I really recommend it.