Dots and Boxes

Players: 2
Ages: 5 and up
Cost: Free!
Math Ideas: Spatial reasoning, logical deduction
Questions to Ask: 
    Is this line safe to draw?
    How can you get more than one box on a single turn?
    How many lines can you draw without capturing a single box?

Sometimes I want a game that will take up an entire hour, the sort of game that can absorb me and my kids on a rainy afternoon. On those days, I reach for Qwirkle or Mastermind.

But other times, I just need a game that will keep my kids occupied for ten minutes while we wait for the dentist to call us back. In those moments, I am looking for a game that is quick, fun, and easy to learn.

Dots and Boxes is a perfect game for these situations. All you need is a pencil and paper (or a crayon and the back of a kid's menu). Of course, knowing me, I've found all sorts of deeper math in this simple game. But first let's just take a look at how the game is played.

How to Play

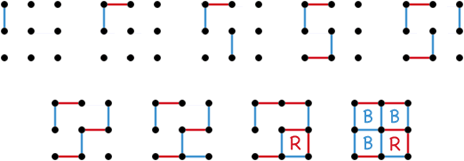
To set up a Dots and Boxes game, you just need a square array of dots. I like to start with four rows of four dots.  Each player takes turns connecting adjacent dots, either vertically or horizontally.

The goal is to claim as many boxes as possible. If you draw the fourth side of a box, you get to claim that square by writing your initials inside (or, if playing with crayons, you can color in the box with your color). If you claim a box, you get another turn, which means you can potentially claim two, three, or even more boxes on a single turn.

The game ends when all lines have been drawn, all boxes have been claimed, and the person with the most boxes wins!

If you'd like, you can watch a quick video tutorial below:

Where's the Math?

The math of Dots and Boxes begins to reveal itself after you play a couple of quick rounds. 

Your child may draw in the third side of a box, only to realize that you can happily claim that box on the next turn. So they begin to look at the game board a little differently, focusing on "safe" lines that they can draw. The beginning of the game turns into a dance, where both opponents circle each other, adding lines in new locations while being careful not to draw the third side on any box, lest their opponent claim that fourth side.

Eventually, of course, someone is going to run out of safe spots to play, and the race for boxes begins in earnest. Then a new question presents itself: How can I claim more than one box in a single turn? 

Your child might begin to notice that if they create little chains of boxes across the board, they can fill in multiple squares on a single turn. For example, in the image below, the blue player is able to capture three boxes in a row by capturing the chain of boxes that runs around the top left corner of the board.
Once you've played a couple of rounds on a 4x4 grid, you should move up to larger grids such as 6x6 or 8x8 so that these chains of boxes become more apparent to you and to your child.

Once you see the chains of boxes, you begin to look at the board with an even more refined perspective on the spatial relationships that the board contains. Each new insight into the strategy of the game allows you to see new things in what would otherwise be a simplistic set of dots and lines. 

By the way, I always recommend that you use an even number of dots in each row of your square grid. Can you (or your child) figure out why?

Questions to Ask

Dots and Boxes is a great game for questions with your kid, since the game is accessible to kids as young as 5 while still being a strategic challenge for teenagers and adults.

For the younger kids, a great question to ask is "Is this line safe to draw?"You can ask this question on your turn or on theirs, with the same goal in mind: getting your child to determine whether a line will allow the opponent to claim a box. This sort of simple, repeated question can help your child hone in on the strategy of the game.

Once your child has the basics down, you can start asking deeper questions to pull out the strategy of the game. A great start is "How can you claim more than one box in a turn?" You can even ask your child to draw a sample game board to show how they can capture multiple boxes at once. Once they can create a chain of boxes on a sample board, they can work toward building those chains in the game!

Lastly, you can always find some sort of puzzle in games like this. Here's a quick one: How many lines can you draw without completing a single box? That's a challenge that you and your child could both try!

Dots and Boxes is a game that helps your child, not with the arithmetic parts of math, but with the geometric and logical elements of math that are the underpinning of so much mathematical development. Considering how under-emphasized these parts of math can be in a typical classroom, this game is a great supplement for kids of all ages.